1.问题

1 ~ n(n+1)/2的整数，排列成类似帕萨卡三角形的等边三角形数阵（从上到下，每行依次有1、2、…、n个数字）, 其中每个不在最后一行的数都恰好等于排在它下面的两个数的差的绝对值。满足这样排列的三角形称为正差三角形（Triangles of Absolute Differences，TAD）。
行数n称作TAD的阶。
有时候，为方便分析，TAD也可以摆成从上到下的每行依次有n、n-1、…、1个数字。为加以区分，尖头朝上的三角形我们称之为正差上三角形（Up-Pointing TAD，UPTAD），尖头朝下的我们称之为正差下三角形（Down-Pointing TAD，DPTAD）。

2.历史

• 1976年，趣味数学家Colonel George Sicherman在观看台球比赛时想到一个问题：比赛开始前先要把数字1-15的台球摆成三角形，那么这15个数字是否可以摆成一个“差值三角形”（difference triangle）呢？即每个数字都是它上面一对数字的正差（positive difference）。Sicherman先是手算出了答案，然后编写Fortran程序分析了任意行数n的情况，不过当时计算机性能有限，很难分析n较大时的情况。研究n=21时，他找到了一个有关奇偶性的简单证明。
• 1977年4月，Sicherman的朋友Martin Gardner把这个问题写进其在《科学美国人》杂志上的《数学游戏》专栏里¹（后来题集成书²时也被收录了进去）。Charles Trigg³详细研究了5阶TAD，并推测: 不存在n>5的TAD。
• 1977年，Herbert Taylor证明：不存在9阶及以上的TAD，但他并未发表该证明。
• 1977年6月，台湾中央研究院Chang, Hu, Lih 和 Shieh四人⁴给出证明：不存在6阶及以上的TAD。
• 2008年，Ian Stewart在书⁵中收录了该题目，名为纸牌三角（Triangle of Cards），用的5阶UPTAD。
• 2010年，第9届 Gathering for Gardner 大会上，Andy Liu等人（有两个作者当时还是初中生和高中生）发表文章⁶，Herbert Taylor的证明重见天日。
• 2015年，纽约时报官博上有一期智力游戏用了这个题目⁷，Sicherman还留言评论提供了很多信息。
• 2018年，第59届国际奥林匹克数学竞赛（IMO）第3题与之有关，称其为反帕斯卡三角形（anti-Pascal triangle）。

3.答案

解是左右镜像：找到一个解，沿三角形中心线左右翻转一下，仍然是解。
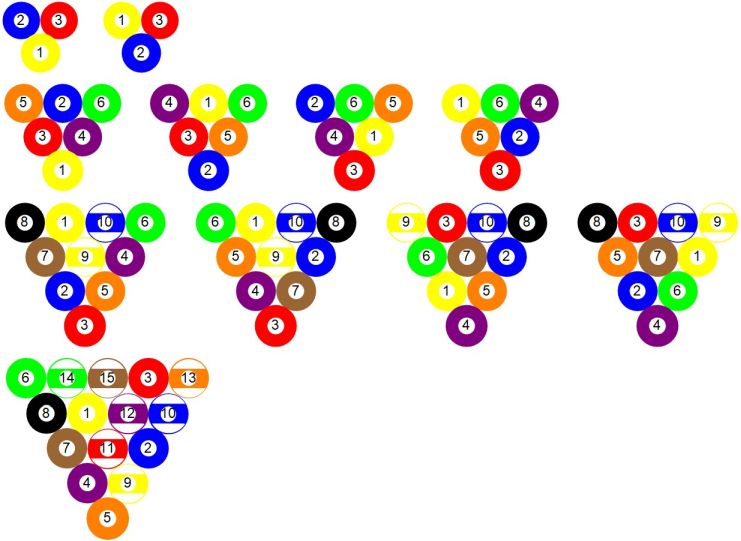
下图列出了所有的DPTAD（不包括镜像的）：

4.BruteFroce求解

UPTAD有两个约束条件：
①总行数为n的差三角，使用1 ~ n(n+1)/2的数字，每个数字仅用1次；
②每行的差分等于前一行。

简单粗暴，直接上所有数字的全排列，自动满足约束条件①；
对每一种可能的排列，DynamicPartition函数将其分割成n行，构造出三角形的形状，DifferenceTriangleQ函数计算每行的差分，判断是否等于前一行，以满足约束条件②。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

DynamicPartition[l_, p_] := MapThread[l[[# ;; #2]] &, {{0}~Join~Most@# + 1, #} &@Accumulate@p];

DifferenceTriangleQ[l_] := Rest[Abs[Differences /@ l]] == Most@l;

DifferenceTriangle[n_] := Module[{max = n (n + 1)/2, allTries},
 Select[DynamicPartition[#, Range@n] & /@ Permutations[Range@max, {max}], DifferenceTriangleQ]];
  
DifferenceTriangle[2] (*4个解*)
{{{1}, {2, 3}}, {{1}, {3, 2}}, {{2}, {1, 3}}, {{2}, {3, 1}}}

DifferenceTriangle[3] (*8个解*)
{{{1}, {3, 4}, {5, 2, 6}}, {{1}, {4, 3}, {6, 2, 5}}, {{2}, {3, 5}, {4, 1, 6}}, {{2}, {5, 3}, {6, 1, 4}}, {{3}, {1, 4}, {5, 6, 2}}, {{3}, {2, 5}, {4, 6, 1}}, {{3}, {4, 1}, {2, 6, 5}}, {{3}, {5, 2}, {1, 6, 4}}}

DifferenceTriangle@4 // AbsoluteTiming (*8个解*)
{73.7682, {{{3}, {2, 5}, {7, 9, 4}, {8, 1, 10, 6}}, {{3}, {4, 7}, {5, 9, 2}, {6, 1, 10, 8}}, {{3}, {5, 2}, {4, 9, 7}, {6, 10, 1, 8}}, {{3}, {7, 4}, {2, 9, 5}, {8, 10, 1, 6}}, {{4}, {1, 5}, {6, 7, 2}, {9, 3, 10, 8}}, {{4}, {2, 6}, {5, 7, 1}, {8, 3, 10, 9}}, {{4}, {5, 1}, {2, 7, 6}, {8, 10, 3, 9}}, {{4}, {6, 2}, {1, 7, 5}, {9, 10, 3, 8}}}}

全排列要对(n(n+1)/2)!种可能进行测试，当n=4时，就将近400万了，给出8个解，耗时1分钟。

4.1 用差优化

UPTAD中的数字并非随机排列，每一行都等于下面一行的差分。所以最后一行定了，上面各行也就定了。
所以，这里我们换个视角，用台球问题的DPTAD形式。
仅需对n(n+1)/2个数字中取n个进行排列，对于n=4，测试数量一下子就降到5040个了。
此时构造出的三角形满足了约束条件②，仍需要对约束条件①进行判断。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

DifferenceTriangle[n_] := Module[{max = n*(n + 1)/2},
   Select[Permutations[Range@max, {n}], DuplicateFreeQ@Flatten@NestList[Composition[Abs, Differences], #, n - 1] &]];

DifferenceTriangle@5 // AbsoluteTiming (*2个解*)
{4.16812, {{6, 14, 15, 3, 13}, {13, 3, 15, 14, 6}}}

PrintTAD[t_] := Column[Grid[{#}] & /@ t, Center];
PrintTAD@NestList[Composition[Abs, Differences], {6, 14, 15, 3, 13}, 4]
6     14     15     3     13
   8      1     12     10
      7     11     2
         4      9
            5

n=6时，测试数量仍然需要近400万。

4.2 用模式优化

即便是第一行，也不是随便取的，有一些规律可循，比如：
①最大数肯定在第1行
②通过第1行每个数字的奇偶性，可以计算整个三角形上所有数字的奇偶性，而这些必然奇偶各半。
先计算奇偶性的模式，测试对象是在{False, True}里选n个的排列，数量仅2^n。
n=6时，数量从近400万一下子降到64个，结果发现没有pattern满足，直接就返回空集，不用再继续求解。

1
2
3
4
5
6
7
8
9

Patterns[n_] := DeleteDuplicates[Select[Tuples[{False, True}, n], Count[Flatten@NestList[Xor @@@ Partition[#, 2, 1] &, #, n - 1], False] == Floor[n (n + 1)/4] &], #1 == Reverse@#2 &];

AllTries[n_] := Module[{p = Patterns@n, max = n*(n + 1)/2}, 
   If[p == {}, {}, Select[Permutations[Range@max, {n}], (MemberQ[#, max] && MemberQ[p, OddQ@#]) &]]];

DifferenceTriangle[n_] := DeleteDuplicates[Select[AllTries@n, DuplicateFreeQ@Flatten@NestList[Composition[Abs, Differences], #, n - 1] &], #1 == Reverse@#2 &];

DifferenceTriangle@5 // AbsoluteTiming
{1.30141, {{6, 14, 15, 3, 13}}}

n=7时，仍然需要测试P(28,7)，近60亿个。

5.数学证明

考虑3阶以上的DPTAD，从最下面那个数字开始往上找，其肩膀上两个数字，较大的那个用粗线连接，较小的那个（叫做脚，为方便起见，第一行的数字也叫做脚）用细线连接。一直到第一行，最大的那个叫做头，所有粗线连接起来叫做脊柱（spine），如下图所示。

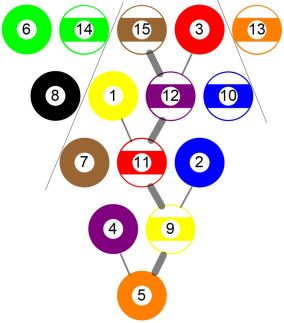
不难证明：头=n(n+1)/2, n只脚是1~n，所有脚加起来等于头，每只脚是其所在行最小的数字。
现在，从第一行的头脚左右两侧 画 三角形两条侧边的平行线，将TAD分成包含脊柱的主三角和左右两侧的副三角，当第一行的头脚两侧尚有空间时会有两个副三角，当头脚偏向一边时则只有一个副三角。
无论哪种情况，副三角（们）共包含n-2只脚。它们的头之和Q ≥ (n+1)+(n+2)+...+(2n-2)=(n-2)(3n-2)/2
由于TAD最大的数n(n+1)/2已经被主三角的头用掉了，所以:
①有1个副三角时，Q ≤ n(n+1)/2-1，与上式联立得n≤3
②有2个副三角时，Q ≤ (n(n+1)/2-1) + (n(n+1)/2-2)，与上式联立得n≤8

数学最可爱的地方就是：当计算机吭哧吭哧算不出来的时候，数学幽幽地来一句：不用算了，哥给你个上限。

参考文献