每个整数都可以分解成若干个质数相乘，即分解质因数。如果需要偶数个质数相乘，我们称其为偶类型（我们定义1也是偶类型），反之则为奇类型。
对于1~10这前10个整数，奇类型有2，3，5，7，8，偶类型有1，4，6，9，10

Ian Stewart的《数学万花筒》称其为奇偶赛马问题（Two-Horse Race），即想象奇马、偶马两匹马赛跑，让它们在同一起跑线上，按数字1、2、3念下去，碰到奇类型，奇马前进一步，反之，偶马前进一步。奇马似乎总是在并排或超前位置，相当形象。

1919年，匈牙利数学家（《怎样解题》作者）George Pólya猜想：对任意自然数n，它以内的所有自然数中奇类型至少占一半。
1958年，Colin Brian Haselgrove证明该猜想是错的。
1980年，Minoru Tanaka用计算机找到最小的反例906,150,257。
测试了9亿多个数字都正确，但保不准下1秒就打脸，就是这么无情残酷无理取闹。
Every number is meaningful and all have their purposes.
万数皆有意，一数一菩提。

下面我们验算一下。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

(*可以直接用LiouvilleLambda，但比这个略慢一些*)
PCType[n_] := If[EvenQ@PrimeOmega@n, 1, -1]; 
blocksize = 10^7; (*分成91组计算，每组1千万*)
blocks = 91;
(bks = ParallelTable[Total[PCType[(i - 1)*blocksize + #] & /@ Range[blocksize]], 
    {i, blocks}];) // AbsoluteTiming
{4023.83, Null}
(*一泻千里*)
acc = Accumulate@bks
{-842, -4510, -5630, -3192, -7608, -3016, -6598, -7132, -2176, -3884, 
-10162, -8592, -11162, -5636, -3244, -7206, -10696, -17010, -15562, 
-11126, -9698, -4922, -6086, -9594, -7970, -9628, -14754, -17252, 
-16346, -16648, -17882, -12168, -11464, -6452, -8508, -4110, -4244, 
-8500, -11184, -11200, -14386, -14942, -19500, -20456, -24366, 
-23732, -22644, -19746, -18196, -18804, -11604, -11950, -10062, 
-7442, -6866, -5544, -6456, -9230, -11014, -15350, -15668, -14892, 
-18936, -20766, -20196, -21820, -22404, -27546, -22948, -25384, 
-27772, -26580, -25558, -25602, -27618, -22166, -15564, -15628, 
-15656, -19292, -17546, -19704, -19386, -19754, -14908, -17416, 
-13780, -12306, -8570, -4630, -4702}

(lastblock = ParallelTable[PCType[(blocks - 1)*blocksize + i],
    {i, blocksize}];) // AbsoluteTiming
{47.6069, Null}
lastacc = acc[[90]] + Accumulate@lastblock;

SelectFirst[lastacc, Positive]
1
FirstPosition[lastacc, 1]
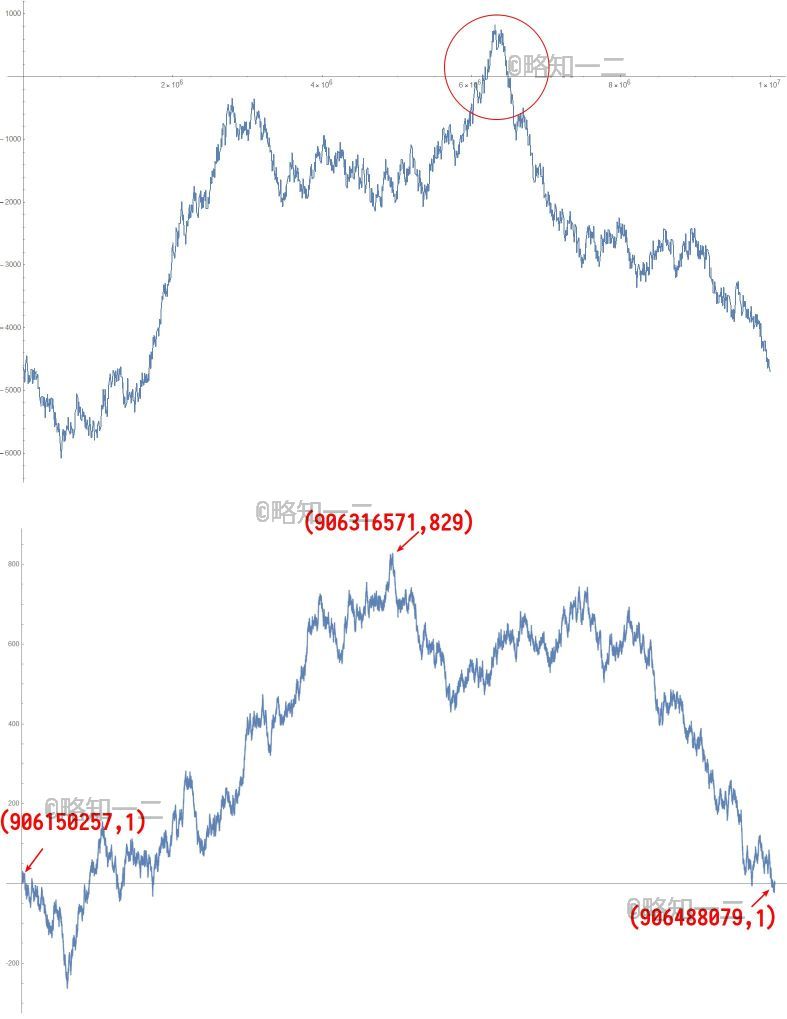
{6150257}
MinMax@lastacc
{-6077, 829}
Count[lastacc, _?Positive]
305426
Position[overall, 1][[{1, -1}]]
{{6150257}, {6488079}}

对于906150257≤n≤906488079之间的305426个整数，偶数马领先，906316571时达到顶峰，领先829位。
但是这种交替领先是否一直存在，即是否在某个数字N之后，只有一种类型马保持持续领先，未知。
polya_conjecture