2020年高考已经结束，本文尝试基于有限的先验知识（读懂题目），用Mathematica软件计算求解题目。

2020年普通高等学校招生全国统一考试 (I卷)
理科数学

一、选择题

1.若 $z=1+i$，则 $|z^2-2z|=$2

Abs[z^2 - 2 z] /. z -> 1 + I

2.设集合 $A=\{ x|x^2-4\le0 \}, B=\{x|2x+a\le0\}$, 且 $A\bigcap B=\{x|-2\le x\le 1\}$, 则 $a=$-2

1
2

Reduce[{2 x + a <= 0, x^2 - 4 <= 0}]
(a <= -4 && -2 <= x <= 2) || (-4 < a < 4 && -2 <= x <= -(a/2)) || (a == 4 && x == -2)

3.埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥， 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为 $\frac{\sqrt{5}+1}{4}$

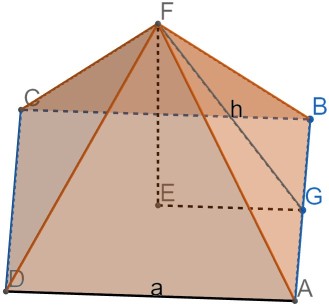
gaokao3

h/a /. Simplify[Solve[{a h/2 + (a/2)^2 == h^2, h > 0, a > 0}], Assumptions -> a > 0]

4.已知 $A$ 为抛物线 $C: y^2=2px(p>0)$ 上一点，点$A$到$C$的焦点的距离为12，到 $y$ 轴的距离为 9，则 p=6

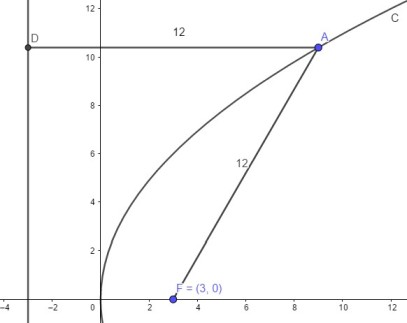
gaokao4

Solve[EuclideanDistance[{9, Sqrt[2 *p *9]}, {12 - 9, 0}] == 12 && p > 0]

5.某校一个课外学习小组为研究某作物种子的发芽率 $y$ 和温度 $x$ (单位：°C) 的关系，在 $20$ 个不同的温度条件下进行种子发芽实验，由实验数据($x_i,y_i)(i=1,2,\dots,20)$ 得到下面的散点图：

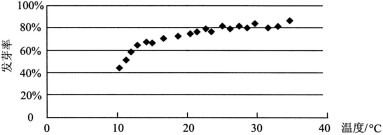
gaokao5

由此散点图，在10°C至40°C之间，下面四个回归方程类型中最适宜作为发芽率 $y$ 和温度 $x$ 的回归方程类型的是: y = a + b ln x​

Fit[{{10, 0.42}, {11, 0.5}, {12, 0.6}, {20, 0.75}, {29, 0.8}, {32, 0.8}}, {1, Log@x, x, Exp[x]}, x]

6.函数$f(x)=x^4-2x^3$ 的图像在点 $(1,f(1))$ 处的切线方程为y=-2x+1

f[x_] := x^4 - 2 x^3; With[{a = 1}, Simplify[f'[a] (x - a) + f[a]]]

7.设函数$f(x)=cos(wx+\pi/6)$在 $[-\pi,\pi]$ 的图像大致如下图，则$f(x)$的最小正周期为4π/3

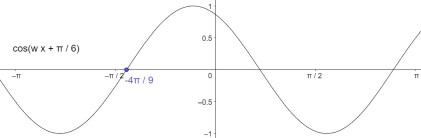
gaokao7

2 Pi/w /. Solve[{Cos[w*(-4 Pi/9) + Pi/6] == 0, Pi < 2 Pi/w < 3 Pi/2}]

8.$(x+\frac{y^2}{x})(x+y)^5$的展开式中 $x^3y^3$ 的系数为15

Coefficient[Expand[(x + y^2/x) (x + y)^5], x^3 y^3]

9.已知 $\alpha \in (0,\pi)$，且 $3cos2\alpha - 8cos\alpha=5$，则 $sin\alpha=\frac{\sqrt{5}}{3}$

FullSimplify[ Sin[a] /. Solve[{3 Cos[2 a] - 8 Cos[a] == 5, 0 < a < Pi}]]

10.已知$A，B，C$为球 $O$ 上的三个点，$\odot O_1$为$\triangle ABC$的外接圆，若$\odot O_1$的面积为$4\pi, AB=BC=AC=OO_1$，则球 $O$ 的表面积为 64π

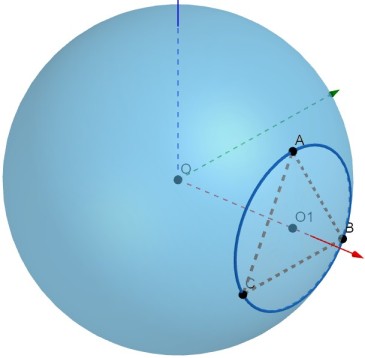
gaokao10

4 Pi ((2 Sqrt[3])^2 + 2^2)

11.已知 $\odot M: x^2+y^2-2x-2y-2=0$，直线 $l: 2x+y+2=0$，$P$ 为 $l$ 上的动点，过点 $P$ 做的切线 $PA，PB$，切点为 $A，B$，当 $|PM|\cdot |AB|$最小时，直线 $AB$ 的方程为2x+y+1=0
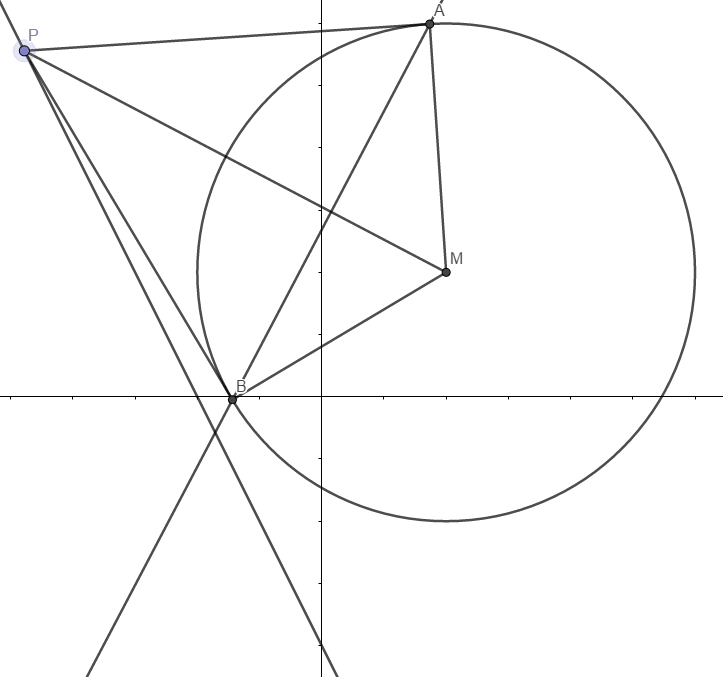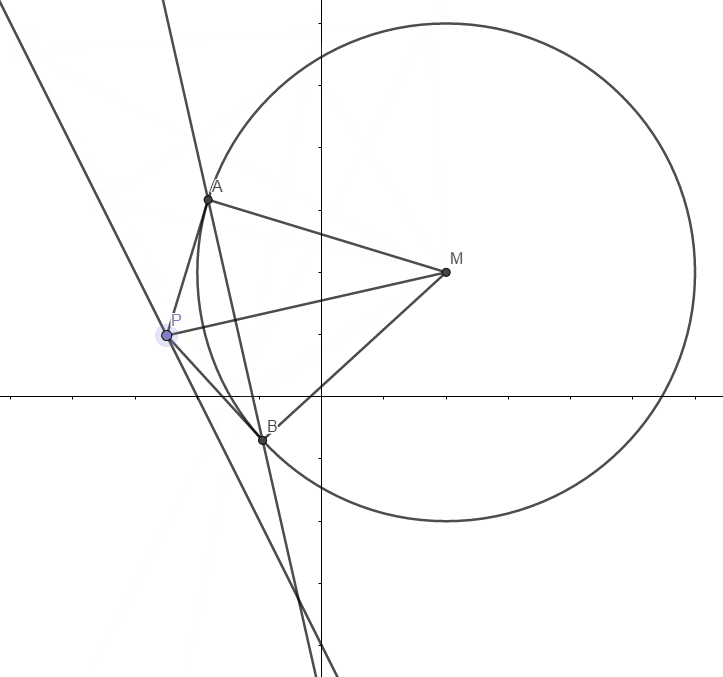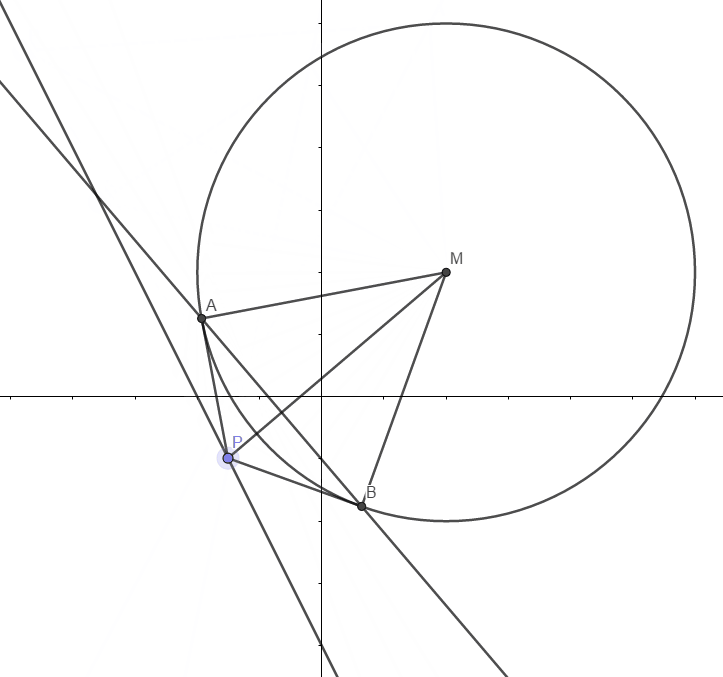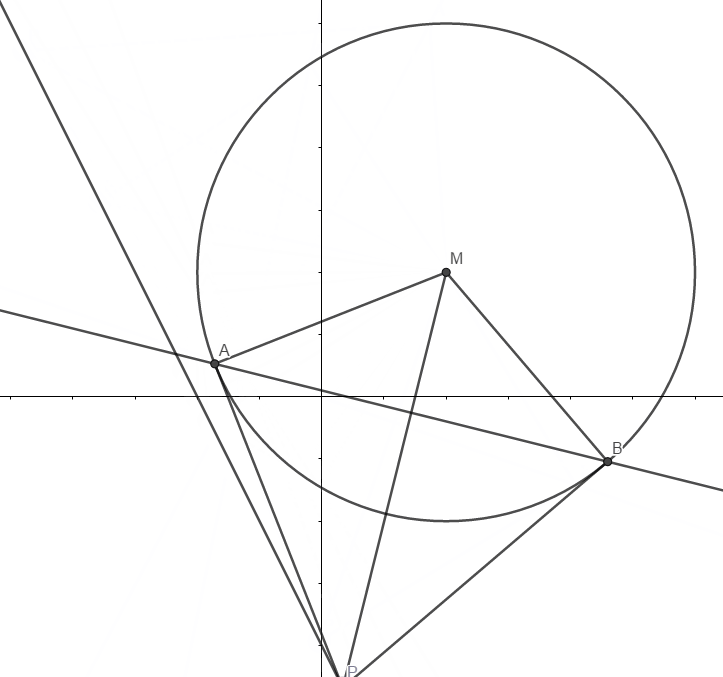
gaokao11

1
2
3
4
5

p = {t, -2 t - 2}; m = {1, 1};
pm = EuclideanDistance[p, m];
t = ArgMin[pm, t];
{a, b} = {x, y} /. Solve[{EuclideanDistance[p, {x, y}]^2 == pm^2 - 2^2, x^2 + y^2 - 2 x - 2 y - 2 == 0}, {x, y}]; 
Simplify[y - InterpolatingPolynomial[{a, b}, x] == 0]

12.若 $2^a +log_2a=4^b+2log_4b$，则a<2b

尚未找到理想的求解方法。不过作为选择题，找到答案没问题。

1
2

f[a_] := b /. FindRoot[2^a + Log[2, a] == 4^b + 2 Log[4, b], {b, 1}]; 
{# < 2 f[#], # > f[#]^2} & /@ Range@5

二、填空题

13.若x，y满足约束条件：$\left \{ \begin{array}{l} 2x+y-2\le0 \cr x-y-1\ge 0 \cr y+1\ge0 \end{array} \right.$，则 $z=x+7y$ 的最大值为1

MaxValue[{x + 7 y, 2 x + y - 2 <= 0, x - y - 1 >= 0, y + 1 >= 0}, {x, y}]

14.设 $\bf a, b$ 为简单向量，且${\bf |a+b|}=1$，则${\bf |a-b|}=\sqrt{3}$

Norm[{ax - bx, ay - by}] /. Solve[{ax^2 + ay^2 == 1, bx^2 + by^2 == 1, Norm[{ax + bx, ay + by}] == 1}]

15.已知F为双曲线$C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 (a>0,b>0)$的右焦点，A为C的右顶点，B为C上的点，且BF垂直于x轴，若AB的斜率为3，则C的离心率为2

1
2
3

f[x_] := b*Sqrt[x^2/a^2 - 1];
c/a /. Simplify[Solve[{f[c] == 3 c - 3 a, c^2 == a^2 + b^2, a > 0, b > 0, c > 0}], 
  Assumptions -> a > 0]

16.如图，在三棱锥P-ABC的平面展开图中，$AC=1，AB=AD=\sqrt{3}, AB \bot AC, AB \bot AD,\angle CAE=30^\circ $, 则$cos\angle FCB=$-1/4

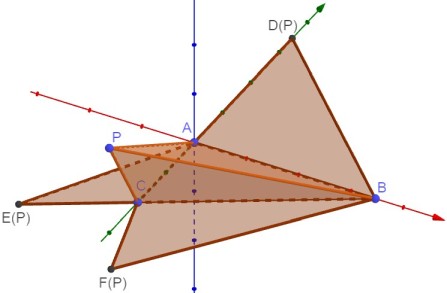
gaokao16

1
2
3
4
5

With[{a = {0, 0, 0}, b = {Sqrt@3, 0, 0}, c = {0, -1, 0}, p = {x, y, z}}, 
 p = {x, y, z} /. First@Solve[{Norm[p - a] == Sqrt@3, 
    VectorAngle[p - a, b - a] == Pi/2, 
    VectorAngle[p - a, c - a] == Pi/6, z > 0}, Reals];
 {Cos[VectorAngle[p - c, b - c]], p}]

三、解答题

17.设${a_n}$是公比不为 $1$ 的等比数列，$a_1$为 $a_2, a_3$ 的等差中项

(1)求${a_n}$的公比 q=-2；

f[n_] := a*q^(n - 1); Solve[{2 f[1] == f[2] + f[3], q != 1}, q]

(2)若 $a_1=1$ ，求数列 ${n a_n}$ 的前 $n$ 项和: $\frac19(1-(3n+1)(-2)^n)$

FullSimplify@Sum[i f[i], {i, 1, n}] /. {a -> 1, q -> -2}

18.如图，$D$ 为圆锥的顶点，$O$ 是圆锥底面的圆心，$AE$ 为底面直径，$AE=AD, \triangle ABC$是底面的内接正三角形，$P$ 为 $DO$ 上一点，$PO=\frac{\sqrt{6}}{6}DO$

gaokao18

(1)证明：$PA$ 垂直于平面 $PBC$

(2)求二面角 $B-PC-E$ 的余弦值: $\frac{2}{\sqrt{5}}$

1
2
3
4
5
6
7

With[{a = {-Cos[Pi/6], -Sin[Pi/6], 0}, 
  e = {Cos[Pi/6], Sin[Pi/6], 0}, 
  b = {Cos[Pi/6], -Sin[Pi/6], 0}, 
  c = {0, 1, 0}, 
  d = {0, 0, Sqrt@3}, 
  p = {0, 0, Sqrt@3*Sqrt@6/6}},
 {VectorAngle[a - p, c - p], VectorAngle[a - p, b - p], Cos[DihedralAngle[{p, c}, {b - c, e - c}]]}]

19.甲、乙、丙三位同学进行羽毛球比赛，约定赛制如下：
累计负两场者被淘汰；比赛前抽签决定首先比赛的两人，另一人轮空；每场比赛的胜者与轮空者进行下一场比赛，负者下一轮轮空，直至有一人被淘汰：当 —人被淘汰后，剩余的两人继续比赛，直至其中一人被淘汰，另一人最终获胜， 比赛结束.
经抽签，甲、乙首先比赛，丙轮空. 设每场比赛双方获胜的概率都为$\frac12$
(1)求甲连胜四场的概率: $\frac{1}{16}$

(2)求需要进行第五场比赛的概率: $\frac34$
(3)求丙最终获胜的概率: $\frac{7}{16}$

构造完整的事件树 $g$，每个结点的值为{{player1, player2}, winlog, loselog}，第一项是比赛双方的索引值(1~3), 第二项winlog是三位同学各自的胜利次数，第三项loselog是三位同学各自的失败次数。
起点 start = {{1, 2}, {0, 0, 0}, {0, 0, 0}};

1
2
3
4
5
6

EndNodes = Select[VertexList@g, VertexOutDegree[g, #] == 0 &];
AllPaths = Flatten[FindPath[g, start, #, Infinity, All] & /@ EndNodes, 1];
Prob[p_] := Total[(1/2)^(Length[#] - 1) & /@ p];
AWin4Paths = Select[AllPaths, (Length[#] == 5 && #[[-1, 2, 1]] == 4) &]; AWin4Paths // Prob
L5Paths = Select[AllPaths, Length[#] == 6 &]; L5Paths // Prob
CWinPaths = Select[AllPaths, #[[-1, 3, 3]] < 2 &]; CWinPaths // Prob

20.已知 $A，B$ 分别为椭圆$E: \frac{x^2}{a^2}+y^2=1 (a>1)$的左右顶点，$G$ 为 $E$ 上顶点，$\vec{AG} \cdot \vec{GB}=8$. $P$ 为直线 $x=6$上的动点，$PA$ 与 $E$ 的另一交点为$C$，$PB$与$E$的另一交点为$D$
(1)求 $E$ 的方程: a=3
A = {-a, 0}; B = {a, 0}; G = {0, 1}; Solve[{(G - A).(B - G) == 8, a > 1}]
(2)证明：直线 $CD$ 过定点: (3/2, 0)

1
2
3
4
5

lineq[{x1_, y1_}, {x2_, y2_}] := FullSimplify[(y - y1)*(x2 - x1) - (x - x1)*(y2 - y1) == 0];
a = 3; P = {6, p};
c = {x, y} /. First@Solve[{x^2/9 + y^2 == 1, lineq[P, A], y != 0}, {x, y}];
d = {x, y} /. First@Solve[{x^2/9 + y^2 == 1, lineq[P, B], y != 0}, {x, y}];
lineq[c, d]

21.已知函数$f(x)=e^x+ax^2-x$
(1)当 $a=1$时，讨论$f(x)$的单调性

1
2

f[x_] := Exp@x + x^2 - x;
Reduce[D[f[x], x] > 0, x]

x>0 增，x<0 减
(2)当 $x\ge 0$时，$f(x)\ge \frac12 x^3+1$,求a的取值范围
Simplify@MaxValue[(-Exp[x] + x + x^3/2 + 1)/x^2, x]
$a\ge \frac{7-e^2}{4}$
22.在直角坐标系$xOy$中，曲线$C_1$的参数方程为$\left \{ \begin{array}{l}x=cos^kt \cr y=sin^kt\end{array}\right.$ ( $t$ 为参数), 以坐标原点为极点，$x$轴正半轴为极轴建立极坐标系，曲线$C_2$的极坐标方程为 $ 4 \rho cos\theta -16\rho sin\theta +3=0$
(1)当 $k=1$ 时，$C_1$是什么曲线？单位圆
Eliminate[{x == Cos[t], y == Sin[t]}, t]
(2)当 $k=4$ 时，求$C_1$与$C_2$的公共点的直角坐标
Solve[Sqrt[y] == 1 - Sqrt[x] && 4 x - 16 y + 3 == 0]
$(\frac14,\frac14)$
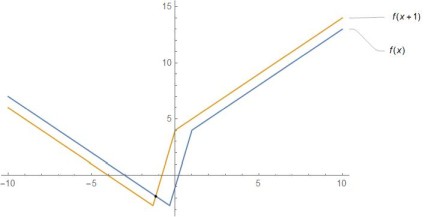
23.已知函数 $f(x)=|3x+1|-2|x-1|$
(1)画出 $y=f(x)$ 的图像
(2)求不等式 $f(x)>f(x+1)$ 的解集

1
2
3

f[x_] := Abs[3 x + 1] - 2 Abs[x - 1]; 
Reduce[f[x] > f[x + 1], x, Reals]
Plot[{f[x], f[x + 1]}, {x, -10, 10}, PlotLabels -> Automatic, Epilog -> Point[{-7/6, f[-7/6]}]]

$x<-\frac76$
gaokao23

图片、源代码文件，公众号回复gaokao2020下载。